Cognitive Learning tells us to clean up our ‘Explicit Instruction Act’
You may already be familiar with the three inner dimensions of the brain’s working memory; the intrinsic load, the extraneous load, and the germane load. Of them all, the extraneous load appears to be the simplest one to ‘get right’. It is to do with the instructional design of the learning episode, i.e. what you (as a teacher) choose to present to learners. In that sense, you have more control over it than the actual content/nature/subject of the ‘curriculum moment’ and the wiring already present in the learner’s brain as they walk through the door. Generally, the extraneous load is thought of in terms of the medium you use to present your input.
The most basic message is ‘don’t provide busy PowerPoint slides’, but the overarching CLT truth is that anything that occupies the brain’s working memory (that is not an integral part of the teaching/learning process) is taking away precious focus. If we look particularly at explicit instruction for primary school mathematics we see that there are more extraneous load factors to consider than just busy slides and making sure the window cleaner doesn’t suddenly appear just as the kids are hanging on your every word and are about to ‘get it’!

Here are three factors to consider that are not part of the physical, distracting ‘stuff’, but are more closely linked to the approach to teaching maths that the school has taken for whatever reason:
Firstly
There is the issue of context. We discourage the approach that automatically places the teaching of a new basic skill for maths in a ‘problem-solving’ context. This overemphasis on an inquiry-based approach is not explicit instruction and does not sit with CLT principles (read more here). If we are about to secure a new step of numeracy progression in Fractions, for example, then the explicit instruction does not need to be hijacked by a context of 3 friends (sometimes with unusual names that add to the distraction) all buying long sandwiches from a well known fast-food sandwich shop and having to divide the sandwiches up. Thoughts of which sandwich fillings and how they are going to cut them may appear to be engaging and meaningful but they are taking up valuable and severely limited working memory capacity.
Hence, such contexts need to be thought through very carefully. Is the trade-off of an increase in extraneous load worth the potential engagement? If we take such problem-solving contexts out of the explicit instruction then we can secure the concept and skill of the new learning with more germane load available. Then we can gradually introduce more challenging contexts to apply the skill to. We are heading to the same problem-solving sandwich shop context, but we will get there quicker! We will also keep more pupils with us, with greater confidence than if we start with the context.

Secondly
By asking novice learners for their ideas (that are made up on the spot), we can find ourselves accepting, encouraging, and even valuing inefficiency. It certainly does not follow the principles of Cognitive Load Theory. It would be damaging enough to the extraneous load if we were presenting multiple new methods simultaneously, but to actually discuss methods created (and presented!) by novice peers on the spot…!
Finally
There is the issue of manipulatives/concrete resources. We discourage approaches that automatically tell teachers to use practical mathematical resources when teaching new calculation skills. Though there are times when this is an essential part of the new content, more often, securing the concept and skill of new learning should precede the introduction of different contexts. Some approaches to primary maths say that because mathematical conceptual progression happens through the broad phases of ‘concrete-pictorial-abstract’ (CPA) that this must dictate every lesson must follow this flow.
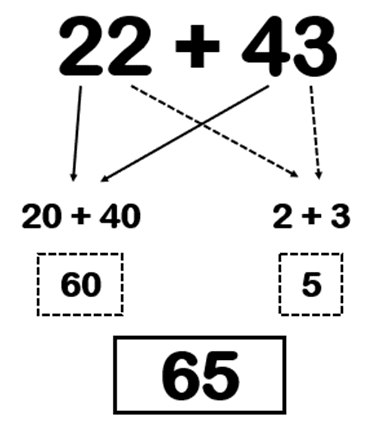
This does not make sense. For example, if a child is learning to calculate ‘2 digit add 2 digit’ (see Using CLT to Crack Addition: Parts 1, 2 and 3) for the very first time in their lives, then it might seem fitting for them to set it out with apparatus (e.g. denes). However, you will notice the emphasis in the posts mentioned that the child is already completely fluent with the pre-requisite skills. This is an important aspect of CLT.
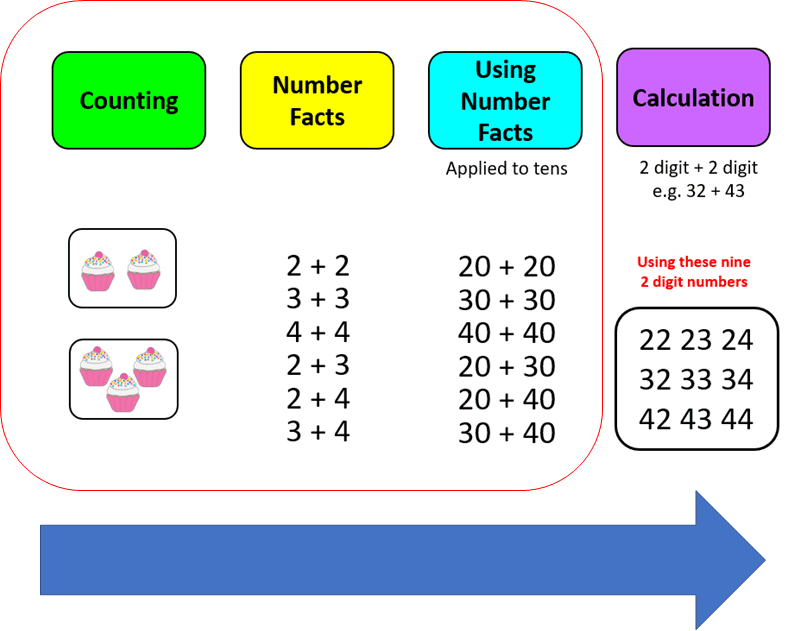
This ‘complete fluency’ means the learner already has a backstory of understanding held in a schema in their Long Term Memory (LTM) that includes ‘feeling and seeing’ the numbers as well as writing out the operations involved. So, just continuing the example, if we have designed a whole-school numeracy journey on the principles of CLT then learners hitting the ‘beautiful moment’ of ‘2 digit add 2 digit’ for the first time have already fully explored (and understood through CPA) the first three stages of the build-up to this calculation shown below; Counting; Number Facts; Using Number Facts; as well as partitioning and recombining a 2 digit number.
This all means that explicit instruction is free of unnecessary visual input (not just in terms of busy PowerPoint slides but images of the concept).
Furthermore, we can, and should connect the ‘2 digit add 2 digit’ skill back into different visual representations (e.g. bar model, 100 square, Numicon, Denes etc.) as part of the ‘deepening process in order to move the learning into LTM. The main point is that any blanket ruling to involve concrete and visual resources in the explicit instruction phase needs to be surrendered to a thoughtful position, especially in light of the need to reduce the extraneous load on the precious capacity of the working memory.

