Using CLT to Crack Addition

Part 1 of 3

Rocking up to teach 30 seven/eight year-old children in an area of high social deprivation where children have been taught Big Maths using CLT to crack addition, the teacher walks straight in and presents a ‘3 digit add 3 digit’ question on screen:

Five seconds later, every single student holds up a little whiteboard displaying the correct answer; having processed the calculation entirely mentally.

Cognitive Load Theory explains how the teacher got to this moment:

First of all, the teacher understood that ‘3-digit add 3-digit’ success isn’t won at the ‘3-digit add 3-digit’ level, but at the ‘2-digit add 2-digit’ level! It might appear that securing steps of progression in basic addition all have equal weighting, but they don’t. ‘2-digit add 2-digit’ is the key step. Why? Because once the skill of ‘2-digit add 2-digit’ is automated in the brain’s Long Term Memory (LTM), all future basic addition steps are easily secured by tagging on to that one process. Once the ‘2-digit add 2-digit’ part of a question comes almost instantly to you, then ‘3-digit add 2-digit’ is easy, you just have to ‘see’ the ‘2-digit add 2-digit’ process and then add on the hundreds amount:

Similarly, assuming the ‘2-digit add 2-digit’ part of a question comes almost instantly, then ‘3-digit add 3-digit’ is easy, you just have to ‘see’ the ‘2-digit add 2-digit’ process and then slot on the quickly totaled, hundreds amount:

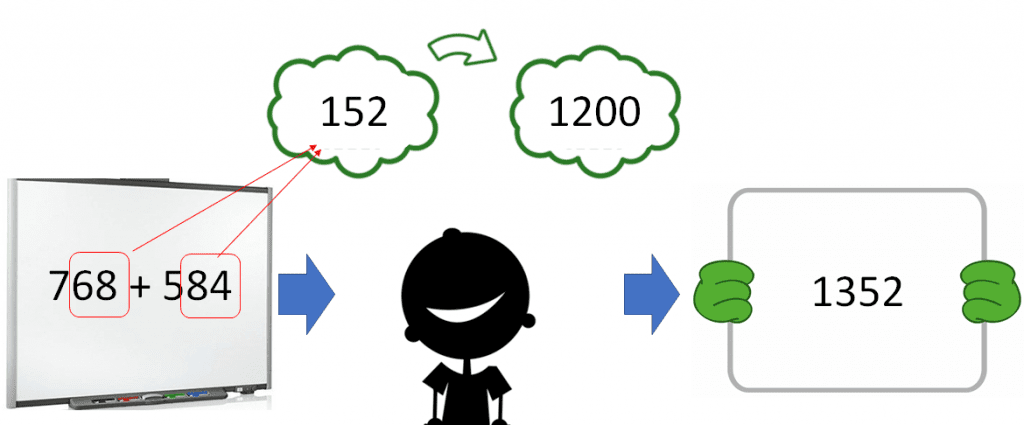
In both cases, the intrinsic load placed on the Working Memory (WM) is vastly reduced by the strength of the ‘2-digit add 2-digit’ schema in the LTM. Indeed, when we build on a strong schema like this it is a win-win; we not only extend the existing original schema, but we also strengthen/modify it as we transfer it into a slightly different context.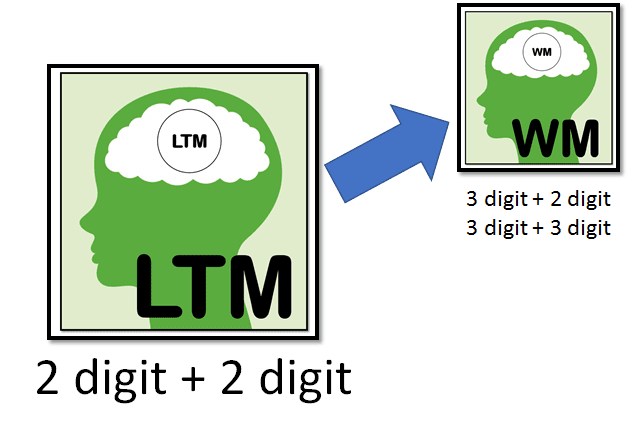 Progressing from a foundation of fluency of ‘2-digit add 2-digit’ to the ability to quickly and mentally calculate any ‘3-digit add 3-digit’ question does not require many sessions/lessons at all (perhaps 2 or 3). However, creating the ‘2-digit add 2-digit’ schema to build on top of, will happen over a much longer time (see (Parts 2 and 3)’).

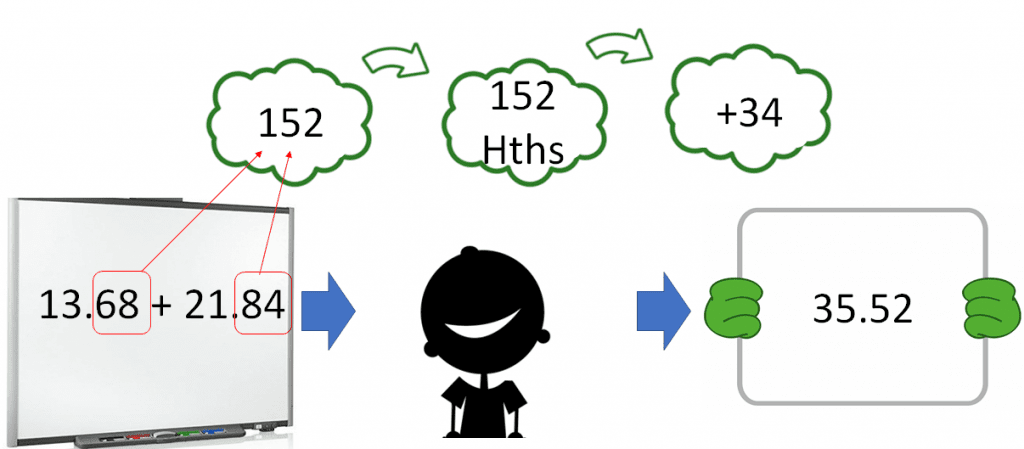
If we jump ahead to a stage on our fluency journey where children have mastered an understanding of hundredths (and 2dp numbers), then they will soon be ready to calculate ‘2dp add 2dp’. This happens by almost instinctively and instantly adding the number of hundredths – since they are 2-digit numbers (albeit 2dp numbers). Notice how, again, the ‘2-digit add 2-digit’ schema vastly reduces the intrinsic load on the WM so that all of the WM focus is being placed on the place value interpretation of the total amount of hundredths (in CLT speak, this is the ‘germane load’).

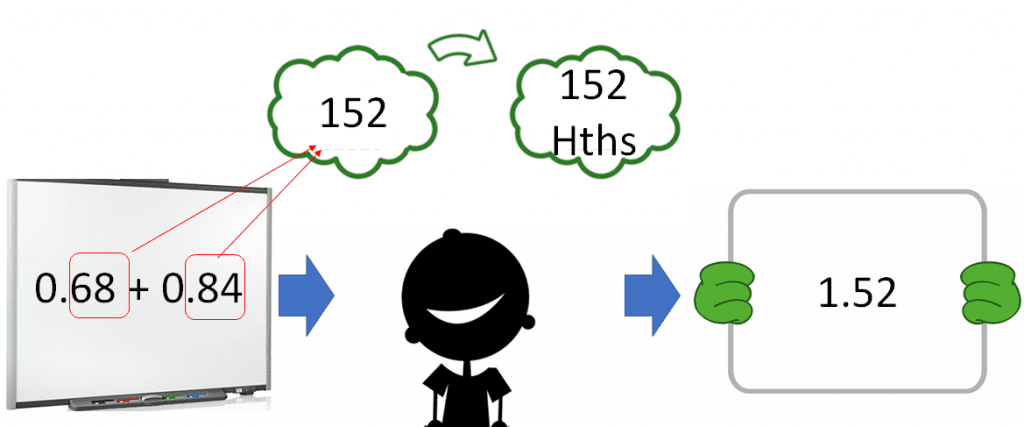
Soon after this process is ‘smoothened off’, students will be ready to include whole numbers too.

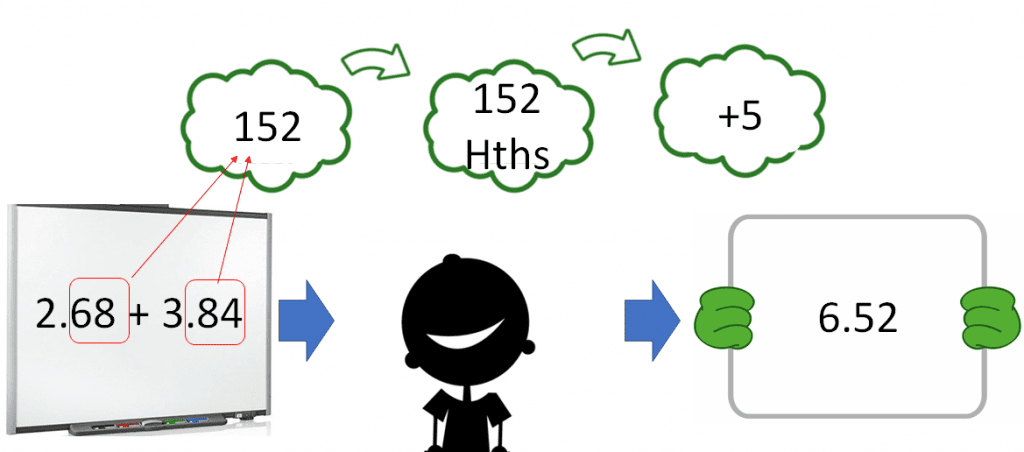
Gradually we can increase the challenge of the whole numbers:

Of course, we have to come back to the point that using CLT to crack addition shows how easy all of this is, and that it will all fall apart if the ‘2-digit add 2-digit’ skill isn’t automated for when any digits are involved (and therefore no matter which addition facts are required). 

There are some further points that spin off this CLT approach of using ‘2-digit add 2-digit’ as the anchor schema in the LTM that makes all future ‘brain only’ addition quick and easy for learners:

• It requires a longer, more thought-out ‘CLT journey to fluency’ than one teacher can be responsible for because it requires teachers in different stages of numeracy development to understand as one and implement together, the CLT-based incremental progression across year groups (see bigmaths.com for such a whole school system).
  
  
• It requires a vision of what it means for primary/elementary-aged children to be properly numerate. In some countries, the national curriculum does not specifically require that children can mentally add 2dp numbers, so the vision of 30 nine/ten year-old children all ‘pinging back’ the answer to such questions is lost. Such schools may need to reclaim the intent of their maths curriculum and see using CLT as the means for ensuring all children become properly numerate in childhood.
  
  
• The same approach of using a common schema anchor to base all future steps of progression exists for Subtraction, Multiplication, and Division (find out more about Big Maths for more details).
  
  
• Intervention: when children are struggling with ‘3-digit add 3-digit’ (and any other addition step beyond it) then CLT tells us that the point of intervention isn’t found by supporting the learner with ‘3-digit add 3-digit’ (even though this would logically appear to be the place to intervene). CLT tells us to go back to the learning gap of the ‘2-digit add 2-digit’ schema, and correct that, before returning to ‘3-digit add 3-digit’.
  
  
• Prevention: with a longer, more thought-out ‘CLT journey to fluency’ that gives quality time to the key schema for each aspect of numeracy (such as ‘2-digit add 2-digit’ for addition), and with strong school leadership to implement such a journey, then there will be no need for intervention. When it comes to learning gaps, prevention is better than cure!
  
  
• Finally, if you were the teacher with 30 students pinging back correct brain-only calculations for 2dp numbers like this, you probably wouldn’t then show them how to solve it by going along columns. It would only slow them down!