Using Cognitive Load Theory to Crack Addition

Part 3 of 3

This is the last of three posts exploring how you use CLT to Crack Addition, and how this can transform your teaching! We suggest you read Part 1 & Part 2 before this post.

We are picking up on children learning to add two 2-digit numbers together for the very first time in their life, and in Part 2 we looked at using Cognitive Load Theory to ensure that the child’s Working Memory (WM) is prepared for this moment. Here is a step-by-step guide to what this episode of explicit teaching looks like:

Step 1

Begin the lesson by quickly revisiting the precise pre-requisite skills that children have already secured fluently but are about to use. In this ‘2-digit add 2-digit’ example, this will include a fast-forward version of the journey we have taken to get here, i.e. the six reduced addition facts, and then a quick recap of their application to the context of ‘tens’; 

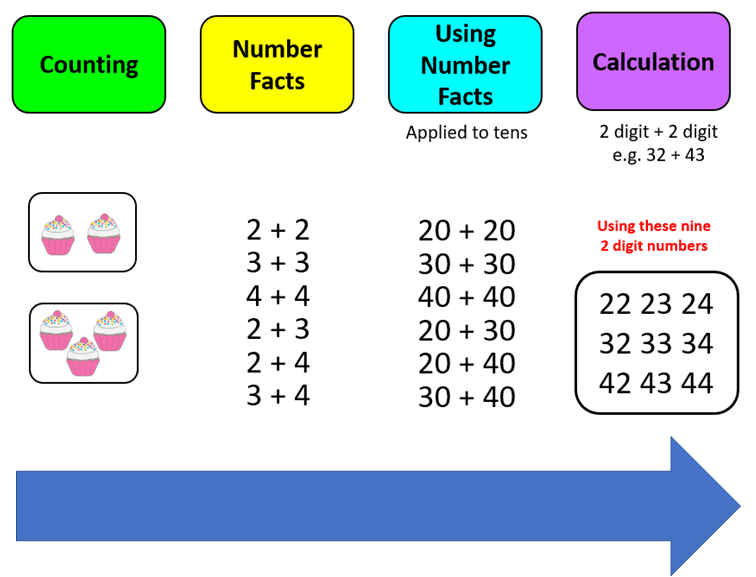
Step 2 – I Do

Model the whole process with a worked example, using ‘out-loud thinking’. This ‘out-loud thinking’ includes modelling the ‘answers’ to the questions you are about to ask (to check understanding); for example, you might say ‘I know 20 + 40 is 60 because I know 2 + 4 = 6 as a fact, and I’ve swapped ones for tens’.

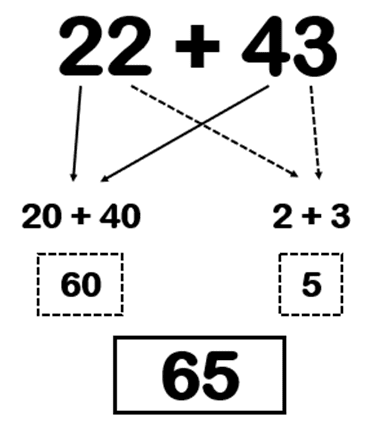
Step 3

Next, clarify the exact process for this new skill, the RT (‘Remember To…’) statements. Again, go through the whole process of the skill, but this time with the RT statements to navigate them.

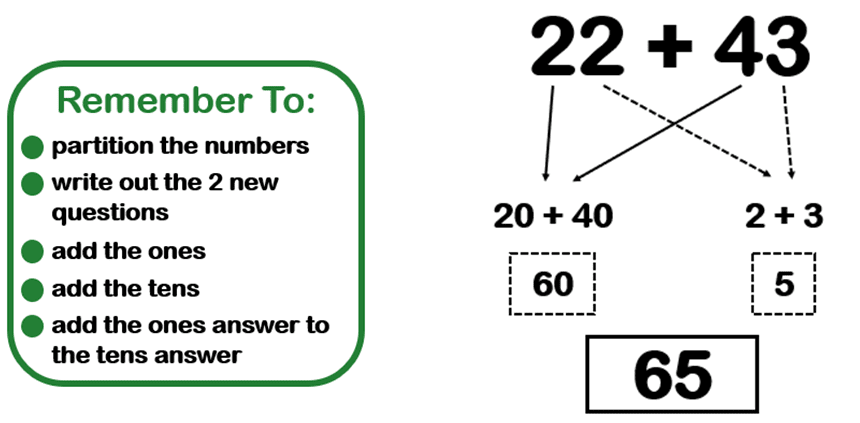
Step 4 – We Do

Having introduced children to and modelled the process (I do), it’s time to go through together, involving the students by bolting on each RT part-skill one at a time. So, initially, it is just the first RT statement, then 1 and 2, then 1, 2, 3, then 1, 2, 3, and 4, and finally the whole process. Each time an extra RT part-skill is bolted onto the process, check in with the children to ensure no one is lost, and that no learning gaps are appearing. This ‘checking in’ has 2 dimensions; doing and understanding.

The ‘doing’ refers to the actual physical skill of drawing out the process with correct numbers in the correct places, thus revealing correct mental processing skills. This necessitates each student holding up their response on a small whiteboard (large clear digits, holding it still with 2 hands under their chin so the teacher can read it and respond if necessary). This assessment moment is akin to a ‘brain scan’ and many teachers enjoy referring to the little boards as ‘brain-scanners’!

The ‘understanding’ dimension is addressed by asking occasionally ‘How do you know?’. For example, ‘How do you know 20 + 40 is 60?’. The child would explain that they have recalled as a fact that 2 + 4 = 6, and merely applied that to ‘tens’. Around 4 or 5 practice questions are given for each build-up stage as each further RT statement is bolted on, until the entire process is complete, when a final 4 or 5 practice questions allow you to check everyone has stayed with you on the journey.

When we use CLT to crack addition, children develop a laminated foundation of understanding that is incredibly strong!

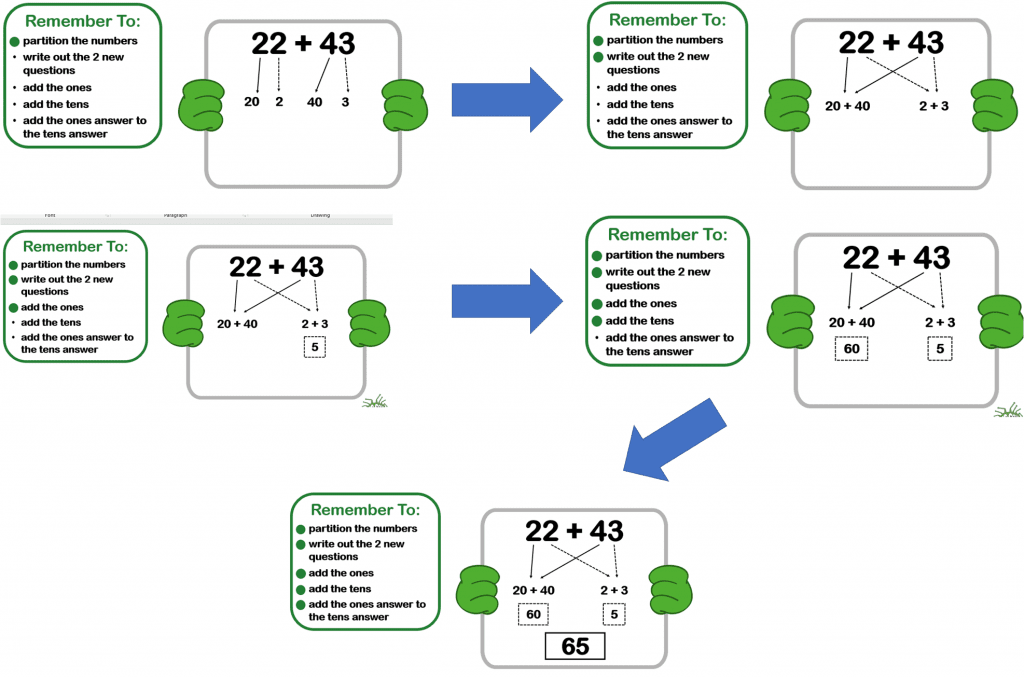
Step 5 – You Do

Once we have supported children through the ‘we do’ phase, our focus changes from communicating the process to helping students to smoothen this process into one smooth skill as they complete it independently several times. When you use CLT to crack addition, it is very much like learning a physical sporting skill such as a tennis serve or a golf swing etc. The part-skills are staccato at first, and the learner is consciously ‘Remembering To…’. It is like cooking a new dish, and only after repeated practice will it become one smooth process that allows it to move into a new category of ‘autopilot’ where other skills can be completed simultaneously. Initially this ‘smoothening off’ means that practice takes place with no further increase in challenge. Continuing to use the same nine 2-digit numbers for our ‘2-digit add 2-digit’ calculations means the germane load of the WM is entirely devoted to the smoothening process. This too should be made explicit to learners as they are encouraged to quicken their process and lean less on the RT statements, which themselves are reflecting the quicker thought process; ‘Come on children let’s go for it; 2 Qs, tens, ones, and pop them back together again!’ As learners succeed in speeding up, then eventually the RT statements disappear. After all, they were really a message to learners to actually remember rather than continuing to read from the scaffold.

Here are some further reflections on this 5 step explicit teaching process:

• The two dimensions of ‘doing’ and ‘understanding’ are both vitally important. They support each other. The more the learner can ‘do’ the more they understand it. The more they understand it, the faster they can ‘do’.

• We can also see in this description how important it is from a pedagogical point of view to avoid having the beautiful ‘CLT moment’ undone by disruptions. Many teachers do indeed face the reality of having learners in the group whose cognitive capacity is immediately overloaded when listening to their input. CLT research tells us that the extraneous load is a major factor in success, and so when the teacher has to constantly break off from the essence of the germane load (in order to address an extraneous issue), the CLT journey to fluency quickly becomes a broken journey. Ensuring all children follow the journey of cognitive preparation (described in Part 2) means a large group of students can hit this moment together.

• When you use CLT to crack addition, the teacher’s is to guide the group (each learner) from ‘a’ to ‘b’. At the start of the lesson, the child has never added two 2-digit numbers together before. By the end of the lesson, they are becoming fluent. As the teacher guides, they respond to each individual. The teacher’s job description at this point is ‘potential learning gap spotter’. The response might well be to keep going with the process as planned because all is well, but that is still a guiding response. This brace of skills, ‘guiding and responding’ is at the heart of great teaching (see  The 5 Megatruths of Great Teaching).

• A whole-school journey to fluency in the basic skills of maths has been set up by the primary/elementary school. The whole-school system is everything. CLT has to work across year groups or it isn’t really working at all. In recent years, teachers’ jobs have changed from ensuring all children make expected progress, to now understanding that children who are ‘off track’ need to be brought ‘on track’. Teachers must accept responsibility for plugging learning gaps that are not ‘their’ responsibility. Now though, CLT encourages schools to set up whole-school systems that ‘build thinking’ in a much more profound way. Therefore the new generation of teachers need not just plug gaps but also identify system faults and be part of a forensic investigation that seeks to identify, address and remedy the fault. In our example, the teacher would ask, ‘How did this child get all this way through our water-tight CLT system without being able to recall these 6 simple addition facts and then apply them to tens?’. To see a whole school primary maths journey designed with CLT underpinning every step then visit www.bigmaths.com.

• We leave this explicit teaching episode with children beginning to smoothen off the skill of ‘2-digit add 2-digit’ but it is not yet a strong and fluent schema in LTM (Long Term Memory) that the teacher can be confident to progress onwards from.

• Only once the 2-digit add 2-digit schema is secured in LTM should we start to inject in new number facts. We move from just using these nine 2-digit numbers to introducing other number facts; same schema, new facts.