Using CLT to Crack Addition
(Part 2 of 3)
If you haven’t read Part 1 of this thread regarding Using CLT to Crack Addition, please do so before reading this post. There is a day in a child’s life when they first learn to solve ‘2-digit add 2-digit’ addition questions. Every child has this day! The child’s teacher wakes with great excitement. This is what it’s all about. Within this day there is an actual moment when the teacher starts their explicit instruction. This will be a beautiful moment since the child’s life is about to change…well, mathematically anyway! There are a lot of steps to teach in a child’s mathematical learning journey and they don’t all have equal weighting; some are more important than others and some are just crucial. This one is one of those crucial ones; tying shoelaces, riding a bike, and ‘2-digit add 2-digit’.
Cognitive Load Theory is a ginormous beast of a pedagogical concept! At times it’s mightily complex and far from being visible in a moment, yet at other times it couldn’t be more simple, more clear, and more beautiful. It is CLT that gets us to this beautiful moment!
Before arriving at this day – this moment…
The children in this class are all going to receive explicit teaching instruction from their teacher on how to add a 2-digit number to a 2-digit number. The teacher knows it is going to go well because they are using CLT to crack addition, so it can’t not. This is the failure-free impact of applying CLT to the teaching of the fundamentals of maths across a primary/elementary school. Before they leave this step of learning these children will be completely fluent with adding two 2-digit numbers ‘brain only’. To begin with, they will only be calculating with nine different 2-digit numbers (22, 23, 24, 32, 33, 34, 42, 43, 44). Only once the skill is automated with these numbers will other numbers be gradually introduced, thus maintaining a manageable load for the WM at all times in terms of number fact recall. Before arriving at this day – this moment – the children will already need to be able to add these numbers:
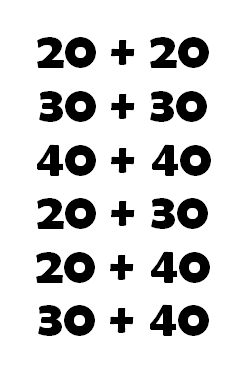 Actually, it’s not quite right to say they need ‘to be able to’, it’s much more accurate to say that they must be fluent with these 6 additions. Of course, our teacher knows that they are already fluent because these children have spent sufficient time developing that fluency. Not only can they instantly respond to these 6 addition questions, but they can also explain the understanding behind their ‘doing’ because their teacher has been using CLT to crack addition. If asked, ‘How do you know 20 + 30 = 50?’ they explain that they are using the fact that 2 + 3 is always 5 and that they are applying it to tens not ones (‘I’ve swapped the thing from ones to tens’ they might say). When first acquiring this understanding they used lots of different mathematical apparatus (including their fingers) to feel the tens, and they have seen lots of different visual representations of the tens. But that is all behind them now. In other words, they have the backstory of understanding locked away in a schema held in the LTM, but for now, if asked ‘20+30?’ they respond immediately and with 100% accuracy…’50!’. Just as you and I would do. Of course, to arrive at this point they have also learned to recall the 6 number facts that sit behind:
Actually, it’s not quite right to say they need ‘to be able to’, it’s much more accurate to say that they must be fluent with these 6 additions. Of course, our teacher knows that they are already fluent because these children have spent sufficient time developing that fluency. Not only can they instantly respond to these 6 addition questions, but they can also explain the understanding behind their ‘doing’ because their teacher has been using CLT to crack addition. If asked, ‘How do you know 20 + 30 = 50?’ they explain that they are using the fact that 2 + 3 is always 5 and that they are applying it to tens not ones (‘I’ve swapped the thing from ones to tens’ they might say). When first acquiring this understanding they used lots of different mathematical apparatus (including their fingers) to feel the tens, and they have seen lots of different visual representations of the tens. But that is all behind them now. In other words, they have the backstory of understanding locked away in a schema held in the LTM, but for now, if asked ‘20+30?’ they respond immediately and with 100% accuracy…’50!’. Just as you and I would do. Of course, to arrive at this point they have also learned to recall the 6 number facts that sit behind: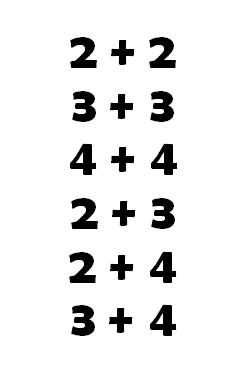 This too has its own backstory. The children have spent time practicing this instant recall, with the explicit instruction to avoid counting out the total; ‘no thinking time’ we say to them. It’s as if they have just been asked to say their own name. When using CLT to crack addition, you learn that to get to this stage the children did indeed start off ‘counting out’ and ‘counting on’ to find the total for themselves. Using everyday items as they played, and then blocks/apparatus, these children have felt, seen, and counted the relationships and rearrangements of these number bonds. They have then been heavily involved with representing them on number lines, number tracks, and number squares. For each one, when they came to just ‘learn it’. the instant recall was cemented onto a schema of understanding:
This too has its own backstory. The children have spent time practicing this instant recall, with the explicit instruction to avoid counting out the total; ‘no thinking time’ we say to them. It’s as if they have just been asked to say their own name. When using CLT to crack addition, you learn that to get to this stage the children did indeed start off ‘counting out’ and ‘counting on’ to find the total for themselves. Using everyday items as they played, and then blocks/apparatus, these children have felt, seen, and counted the relationships and rearrangements of these number bonds. They have then been heavily involved with representing them on number lines, number tracks, and number squares. For each one, when they came to just ‘learn it’. the instant recall was cemented onto a schema of understanding: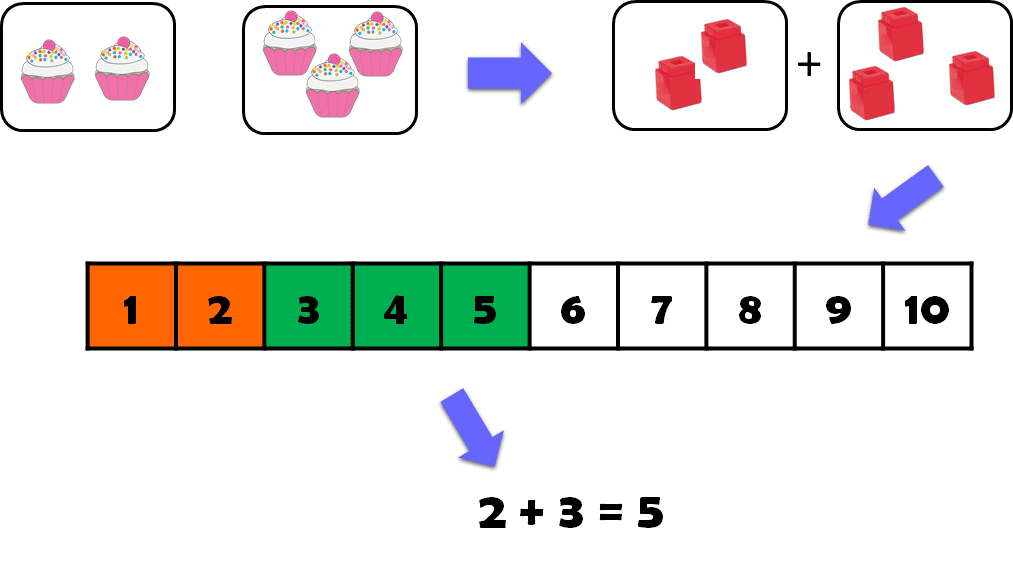
The teacher also knows the children are fluent with partitioning and recombining the 2-digit numbers that they will be using.
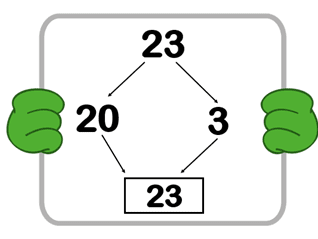
In fact, they are already fluent with the wider process of splitting a number into two parts (tens and ones) operating on each part separately, but consistently, and then recombining the two parts to therefore achieve an overall operation on the original number. In a well-thought-through CLT journey, doubling a 2d number in this way is an earlier learning step.
This is what CLT teaches us; if we want to ensure all children will secure this new skill, with understanding, then our job is to set them up for this beautiful moment. Our excited teacher knows this lesson is going to go well because they are using CLT to crack addition. Each child’s LTM has strong schema fluency of all the pre-requisite skills needed for this beautiful moment when the door to the rest of their numeracy life opens! The cognitive load on the WM is now reduced to just the connecting of previously secured (i.e. already-fluent) part skills. This reduces the ‘intrinsic load’ of the learning as much as possible. So long as we now maintain zero distractions (i.e. reduce the ‘extraneous load’ on the WM to nil) then we have the highest possible WM focus on the targeted mental processes (known as the ‘germane load’) of the new ‘2-digit add 2-digit’ skill. The actual combined process that the teacher will guide the learners through in a worked example is to:
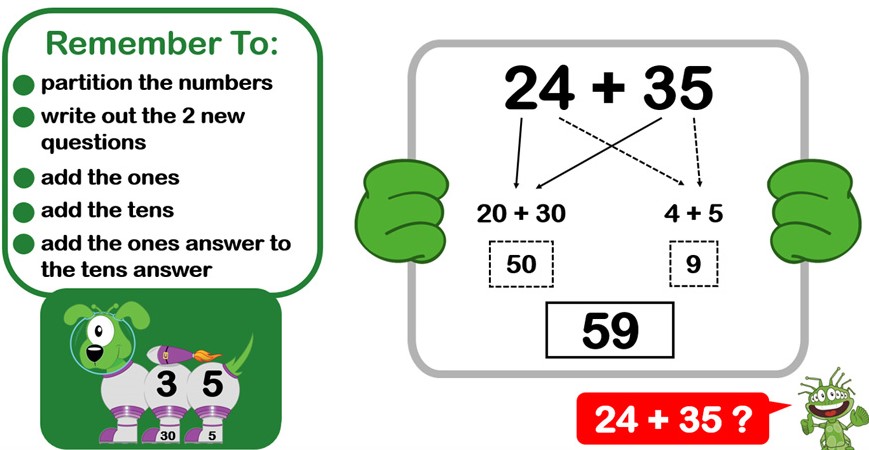
If you are interested in seeing how this process is condensed into the actual explicit teaching moment, and how the process is transferred from teacher to learner, then check out my blog that naturally follows this one (Using Cognitive Load Theory to Crack Addition! (Part 3)). Just for now though, note that these mini-steps are not all separated items in the WM. For example, the first two bullet points are one smooth movement (seeing one question as two, which is itself an existing schema in the LTM, initially established through doubling a 2-digit number).
Some final points:
Success is whole-school or not at all!: You can see that ‘getting the load right’ is a whole school issue. Chronology is everything. Not just within a lesson, a week, a term, a year, but over the years. So, whilst CLT signposts teachers to a much more detailed curriculum journey, it also shows there are massive implications for school leaders when we see how important it is to have one big CLT maths journey from start to finish. To see a whole school primary maths journey designed with CLT underpinning every step then visit www.bigmaths.com.
Reduced number facts!: You probably noticed that only 6 addition number facts are used for the preparation of the CLT beautiful moment for addition. These same 6 facts will be used in the actual explicit instruction, and this too will indeed be made explicit to the learners, i.e. they will be told that only these nine 2-digit numbers will be used in the worked examples. With a predictable bank of part-skills, both teacher and learner can be certain that the WM focus will be solely on the knitting together of the already-fluent part skills.
Reduce the spread!: Of course, if sat listening to explicit instruction, some children are not cognitively ready for this learning episode, then those learning gaps will be exposed and the load on that child’s WM will be too great. Alternatively, any child that is already fluent with ‘2 digit add 2 digit’ will also have their time wasted and again learning has failed. This input is pitch-perfect for this CLT moment. Of course the more children ‘off-track’ (and that is a specific ‘CLT journey to fluency’ track that lives in this moment, not a broader government-driven age-related expectation) then the more distractions from the moment the teacher has and the more extraneous load increases. Everything possible has to be done in the setting up and implementation of the bigger maths journey to avoid a mixed-ability set of learners being involved in this instruction.
Intervention!: If you teach learners over the age of 7/8 years, and they can’t instantly calculate ‘2-digit add 2-digit’, or any addition step beyond that, then it may be helpful to look at this beautiful CLT moment and go back through the journey using CLT to crack addition. Start with those 6 number facts as a point of initial assessment. If the learner can’t recall all 6 totals with instant recall then work on that. However, if they can, then apply it to tens and move forward from there. Once that is secure then they will be ready for this moment…and then the journey beyond!

